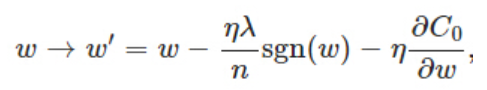在機(jī)器學(xué)習(xí)以及深度學(xué)習(xí)中我們經(jīng)常會看到正則化這一名詞,下面就淺談一下什么是正則化?以及正則化的意義所在?
一、什么是正則化?
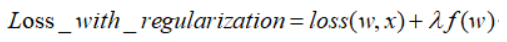
正則化項 (又稱懲罰項),懲罰的是模型的參數(shù),其值恒為非負(fù)
λ是正則化系數(shù),是一個超參數(shù),調(diào)節(jié)懲罰的力度,越大則懲罰力度越大。
二、正則化的目的?
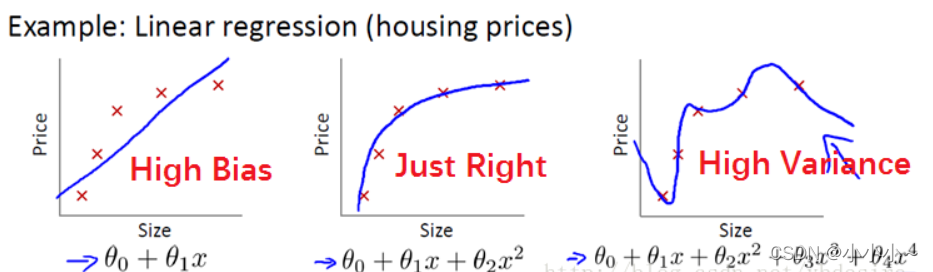
先上圖:
上圖從左到右依次為:欠擬合、理想狀態(tài)、過擬合
欠擬合從字面意思來看就是欠缺擬合程度,這一般在復(fù)雜度很低的模型中出現(xiàn)。從數(shù)學(xué)上來看,一元一次函數(shù)為一條直線、一元二次函數(shù)為一個曲線,以此類推。那么參數(shù)越多,其越能擬合更復(fù)雜的特征,但是一味的增加模型的復(fù)雜度就會造成過擬合現(xiàn)象。一旦過擬合,模型的泛化能力以及魯棒性將特別差。那么怎么結(jié)局過擬合現(xiàn)象呢?
在從數(shù)學(xué)方面分析來看,為了減小過擬合,要將一部分參數(shù)置為0,最直觀的方法就是限制參數(shù)的個數(shù),因此可以通過正則化來解決,即減小模型參數(shù)大小或參數(shù)數(shù)量,緩解過擬合。
在神經(jīng)網(wǎng)絡(luò)中,激活函數(shù)(以sigmoid為例)如下圖
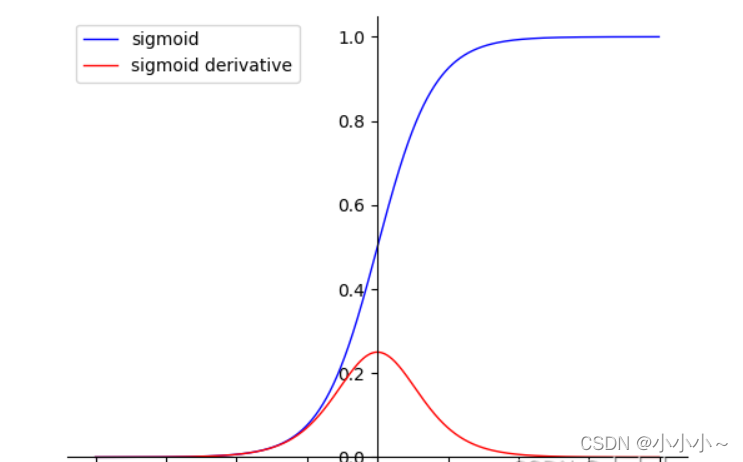
如果我們的正則化系數(shù)(lambda)無窮大,則權(quán)重w就會趨近于0。權(quán)重變小,激活函數(shù)輸出z變小。z變小,就到了激活函數(shù)的線性區(qū)域,從而降低了模型的非線性化程度。
三、L1和L2正則化
(一)L1正則化
L1正則化,又稱Lasso Regression,是指權(quán)值向量w中各個元素的絕對值之和。比如 向量A=[1,-1,3], 那么A的L1范數(shù)為 |1|+|-1|+|3|。
L1正則化可以讓一部分特征的系數(shù)縮小到0,所以L1適用于特征之間有關(guān)聯(lián)的情況可以產(chǎn)生稀疏權(quán)值矩陣(很多權(quán)重為0,則一些特征被過濾掉),即產(chǎn)生一個稀疏模型,可以用于特征選擇。L1也可以防止過擬合。
那么L1為什么會產(chǎn)生一個稀疏權(quán)值矩陣呢?
L1正則化是權(quán)值的 絕對值之和,所以L1是帶有絕對值符號的函數(shù),因此是不完全可微的。機(jī)器學(xué)習(xí)的任務(wù)就是要通過一些方法(比如梯度下降)求出損失函數(shù)的最小值。當(dāng)我們在原始損失函數(shù)后添加L1正則化項時,相當(dāng)于對損失函數(shù)做了一個約束。
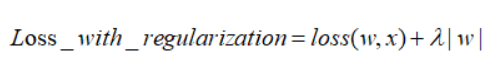
此時我們的任務(wù)變成在約束下求出取最小值的解。考慮二維的情況,即只有兩個權(quán)值和 ,此時對于梯度下降法,求解函數(shù)的過程可以畫出等值線,同時L1正則化的函數(shù)也可以在二維平面上畫出來。如下圖:
(1)、從優(yōu)化問題來看
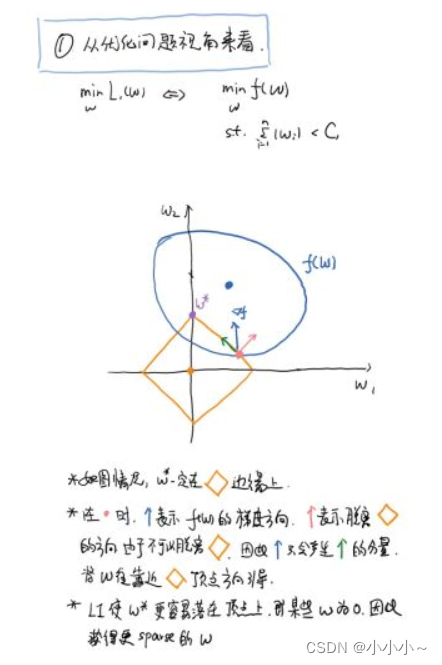
上面的圖不是很清楚,補充如下:
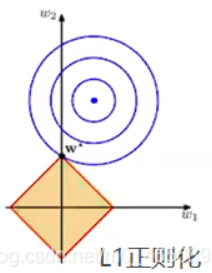
圖中藍(lán)色圓圈線是Loss中前半部分待優(yōu)化項的等高線,就是說在同一條線上其取值相同,且越靠近中心其值越小。
黃色菱形區(qū)域是L1正則項限制。帶有正則化的loss函數(shù)的最優(yōu)解要在黃色菱形區(qū)域和藍(lán)色圓圈線之間折中,也就是說最優(yōu)解出現(xiàn)在圖中優(yōu)化項等高線與正則化區(qū)域相交處。從圖中可以看出,當(dāng)待優(yōu)化項的等高線逐漸向正則項限制區(qū)域擴(kuò)散時,L1正則化的交點大多在坐標(biāo)軸上,則很多特征維度上其參數(shù)w為0,因此會產(chǎn)生稀疏解;而正則化前面的系數(shù),可以控制圖形的大小。越小,約束項的圖形越大(上圖中的黃色方框);越大,約束項的圖形就越小,可以小到黑色方框只超出原點范圍一點點,這是最優(yōu)點的值中的可以取到很小的值。
(二)、L2正則化
L2正則化是指權(quán)值向量中各個元素的平方和然后再求平方根,對參數(shù)進(jìn)行二次約束,參數(shù)w變小,但不為零,不會形成稀疏解 。它會使優(yōu)化求解穩(wěn)定快速,使權(quán)重平滑。所以L2適用于特征之間沒有關(guān)聯(lián)的情況。
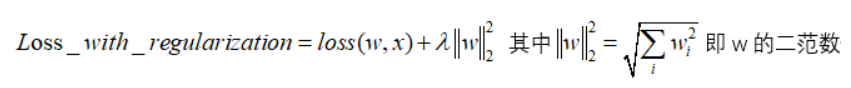 考慮二維的情況,即只有兩個權(quán)值和 ,此時對于梯度下降法,求解函數(shù)的過程可以畫出等值線,同時L1正則化的函數(shù)也可以在二維平面上畫出來。如下圖: 考慮二維的情況,即只有兩個權(quán)值和 ,此時對于梯度下降法,求解函數(shù)的過程可以畫出等值線,同時L1正則化的函數(shù)也可以在二維平面上畫出來。如下圖:

圖中藍(lán)色一圈一圈的線是Loss中前半部分待優(yōu)化項的等高線,就是說在同一條線上其取值相同,且越靠近中心其值越小。圖中黃色圓形區(qū)域是L2正則項限制。帶有正則化的loss函數(shù)的最優(yōu)解要在loss函數(shù)和正則項之間折中,也就是說最優(yōu)解出現(xiàn)在圖中優(yōu)化項等高線與正則化區(qū)域相交處。從圖中可以看出,當(dāng)待優(yōu)化項的等高線逐漸向正則項限制區(qū)域擴(kuò)散時L2正則化的交點大多在非坐標(biāo)軸上,二維平面下L2正則化的函數(shù)圖形是個圓,與方形相比,被磨去了棱角。因此與相交時使得或等于零的機(jī)率小了許多,這就是為什么L2正則化不具有稀疏性的原因。
四、兩種正則化的不同
(一)、從梯度方面來看
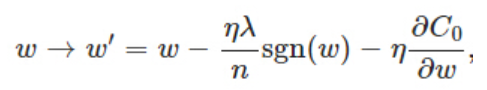

上圖分別為(左側(cè))L1、(右側(cè))L2正則化的反向傳播函數(shù)
相對于L1:比原始的更新規(guī)則多出了η ∗ λ ∗ s g n ( w ) / n η * λ * sgn(w)/nη∗λ∗sgn(w)/n這一項。當(dāng)w為正時,更新后的w變小。當(dāng)w為負(fù)時,更新后的w變大——因此它的效果就是讓w往0靠,使網(wǎng)絡(luò)中的權(quán)重盡可能為0,也就相當(dāng)于減小了網(wǎng)絡(luò)復(fù)雜度,防止過擬合。
相對于L2:在不使用L2正則化時,求導(dǎo)結(jié)果中w前系數(shù)為1,現(xiàn)在w前面系數(shù)為 1 − η λ / n 1−ηλ/n1−ηλ/n ,因為η、λ、n都是正的,所以 1 − η λ / n 1−ηλ/n1−ηλ/n小于1,它的效果是減小w,這也就是權(quán)重衰減(weight decay)的由來。當(dāng)然考慮到后面的導(dǎo)數(shù)項,w最終的值可能增大也可能減小。更小的權(quán)值w,從某種意義上說,表示模型的復(fù)雜度更低,對數(shù)據(jù)的擬合剛剛好(這個法則也叫做奧卡姆剃刀),而在實際應(yīng)用中,也驗證了這一點,L2正則化的效果往往好于未經(jīng)正則化的效果。
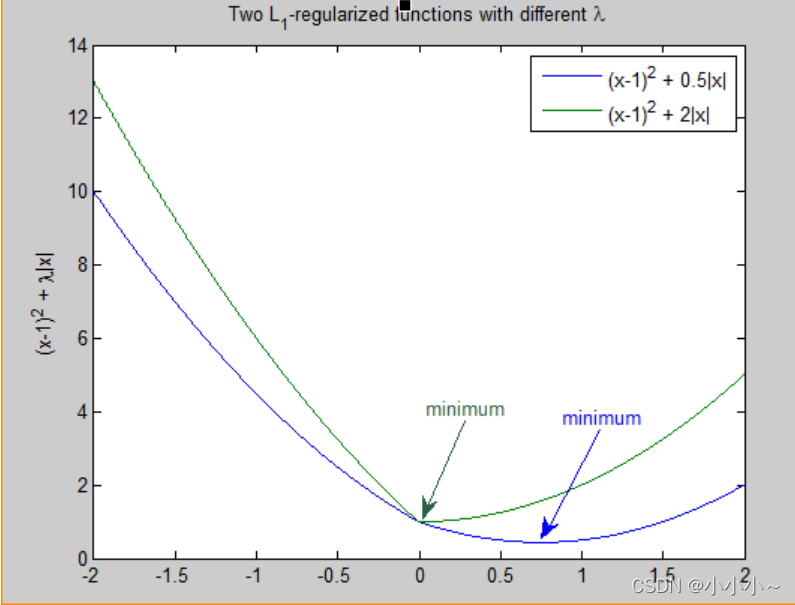
綜合以上兩個式子:當(dāng)w ww處于[ 1 , + ∞ ] [1, +\infty][1,+∞]時,L2比L1獲得更大的減小速率,而當(dāng)w ww處于( 0 , 1 ) (0,1)(0,1)時,L1比L2獲得更快的減小速率,并且當(dāng)w越小,L1更容易接近到0,而L2更不容易變化。下圖反應(yīng)的更為形象一些。
(二)、概率方面來看

| 
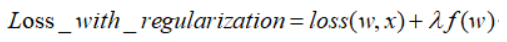


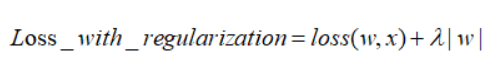


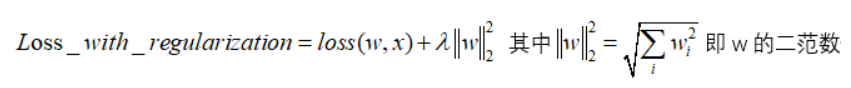 考慮二維的情況,即只有兩個權(quán)值和 ,此時對于梯度下降法,求解函數(shù)的過程可以畫出等值線,同時L1正則化的函數(shù)也可以在二維平面上畫出來。如下圖:
考慮二維的情況,即只有兩個權(quán)值和 ,此時對于梯度下降法,求解函數(shù)的過程可以畫出等值線,同時L1正則化的函數(shù)也可以在二維平面上畫出來。如下圖: